The orth concept in 2D geometry and graphics is where, given some vector, we find a vector (line) that is at right angles to the original. We have a tiny bit of choice about how to do it – we can pick a vector to the left, or to the right – but it’s very simple (more here).

The equivalent function in 3D is one of those odd little problems where you are given some freedom with the answer, and you don’t really care about that freedom – just pick something please! – but you’re made to care about it anyway and do what feels like too much thinking. Bah!¹

I want to mention the concept of walkabout and then go for a meander with the ohmaps idea. The idea is to eventually look at if the ohmap extends from resistance (DC behaviour circuits) to impedence (AC circuits) in any useful way.

I introduced ohmaps in parts 1 and 2 and looked at some simpler examples.

We looked at parallel and series resistor networks (and combinations of those):

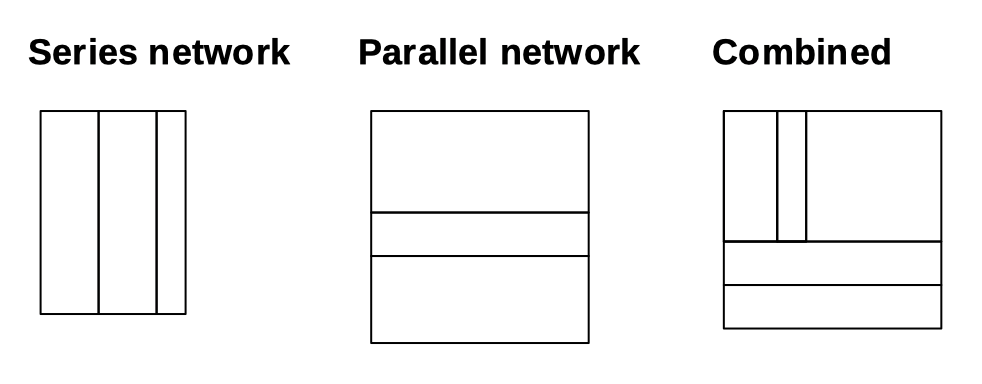
And I wrote this:

And not every resistor network can be shown as an ohmap – things outwith simple series/parallel nestings, like delta or Y networks.

It turns out I was a little hasty here. So how might ohmaps cope with more interesting networks?

I used JLCPCB to fabricate my cap-fun circuit (see part 1). It was under $20 including delivery, for 75 copies of this small PCB (4 x 4 cm).

I’ve been meaning to look into PCB fabrication forever, and it’s time, baby.

What would I make for my first small PCB? I settled on designing an educational demo board for capacitors. I call it cap-fun.

Capacitor demo boards are nothing new, but I’ve remixed things a little because the usual designs hide some nuances of capacitors that I think can be easily demonstrated.

Below I list my amateur radio hardware, it doesn’t represent a single rig!

A recent news story was about doctors not knowing the basics of Bayes’ theorem: they were asked a basic question about false results on a disease test. A lot of them flubbed it.

Let’s be fair: I wouldn’t expect most doctors to be able to regurgitate Bayes law or do an applied example.

I would expect them to say “That question is more complex than it sounds”, rather than fall into the usual trap.

It’s the old knowing what you don’t know (and that’s for another post).

Anyway, that was the prod for me do a dive into basics of Bayesian Analysis in several parts.

I’ve exhibited at Colony of Artists several times, a vibrant art festival at Abbeyhill Colonies in Edinburgh.

One of the things I was showing and selling was my tesselation pieces: designs inspired by MC Escher’s work, particularly matamorphosing tesselations.

Some of these pieces play with negative space and the transition from 3D to 2D:

These are notes from a workshop I gave on Snare technique for Beltane 2021 (Acropolyptic).

The target audience is someone learning basic technique from the ground up, particularly in the context of processional drumming (playing a single drum). But the skills can equally apply to kit drumming etc.

Developing snare technique is hard. It can take ten hours or more practice time to start solidifying things, due to the fine motor control and muscle memory training involved.

Sometimes I do some GLSL or similar: much graphics and geometry. I usually scribble down some back-of-envelope variant of the usual geometry equations, but I’ve never consistently decided what to call things or how to write them down.

Here I’m setting down the notation I’m going to use, and capturing the definitions. Reference pseudo-implementations are given too (Swift).

The equations and source given here have been unit tested; full source to come after tidying.