Orthogonal flight path intersection: my own solution
After seeing my post on ChatGPT dazzle, a friend asked what the code for that exact problem would look like if I rewrote it in a better way.
I did criticise the original code, so it’s fair that I should show my own version.
Below is my solution for almost the same problem.1 In my solution I’m returning the time difference between the two particles hitting the flight paths’ intersection point, because that’s much more useful than hard-coding in a notion of ‘did hit/didn’t hit’ based on tiny numbers.
def miss_time_for_intersection_point(A_0, A_v, B_0, V):
# B_0 - A_0
start_delta = (B_0[0] - A_0[0], B_0[1] - A_0[1])
start_delta_mag_sq = start_delta[0]**2 + start_delta[1]**2
A_v_mag = sqrt(A_v[0]**2 + A_v[1]**2)
A_v_unit = (A_v[0] / A_v_mag, A_v[1] / A_v_mag)
# dot(start_delta, A_v_unit)
A_i = start_delta[0]*A_v_unit[0] + start_delta[1]*A_v_unit[1]
B_i = sqrt(start_delta_mag_sq - A_i * A_i)
A_t = A_i / A_v_mag
B_t = B_i / V
intersect_time_diff = abs(B_t - A_t)
return intersect_time_diff
Example invocation:
A_0 = (-1.0, 0.0) # A starting point
A_v = (0.5, 0.0) # A velocity
B_0 = (0.0, 10.0) # B starting point
V = 1.0 # B velocity (in direction of flight paths intersection)
print(f"Time gap between A, B passing intersection point: ")
# outputs 8.0
print(miss_time_for_intersection_point(A_0, A_v, B_0, V))
If you set things up so that A is travelling away from the intersection (i.e. the intersection is in the past), it still works. For example, set A_0 = (1, 0) and you’ll get the answer 12.
If we rewrite the code as pseudo-code that uses a vector helper, you can grok that the maths is fairly simple:
def miss_time_for_intersection_point(A_0, A_v, B_0, V):
start_delta = B_0 - A_0
start_delta_mag_sq = magnitude_squared(start_delta)
A_v_mag = magnitude(A_v)
A_v_unit = unit(A_v)
A_i = dot(start_delta, A_v_unit)
B_i = sqrt(start_delta_mag_sq - A_i**2)
A_t = A_i / A_v_mag
B_t = B_i / V
intersect_time_diff = abs(B_t - A_t)
return intersect_time_diff
My code (both original form and the pseudocode) is 9 lines long. Compare that to the 35 lines of code in the tweet.
So my version is a quarter of the size.1
Note also that if our function is passed a unit vector for \(A_v\), it gets even simpler – 6 lines of code (17% of the tweeted GPT code):
def miss_time_for_intersection_point(A_0, A_v_unit, B_0, V):
start_delta = B_0 - A_0
start_delta_mag_sq = magnitude_squared(start_delta)
A_i = dot(start_delta, A_v_unit)
B_i = sqrt(start_delta_mag_sq - A_i**2)
B_t = B_i / V
intersect_time_diff = abs(B_t - A_i) # A_t = A_i when A_v is a unit vector
return intersect_time_diff
The problem breakdown
Here’s a quick summary of the thinking that led to the above code.
Stating the problem:
Two particles A and B are in linear motion in 2d. B is travelling orthogonally (right angle) to A.
A has start position \(A_0\) and velocity \(A_v\).
B has start position \(B_0\) and speed \(V\) towards the path intersection.
What is \(t\), the time elapsed between the particles passing the path intersection point?
If you sketch out what’s going on, you get a nice right-angled triangle due to the orthogonal travel requirement:
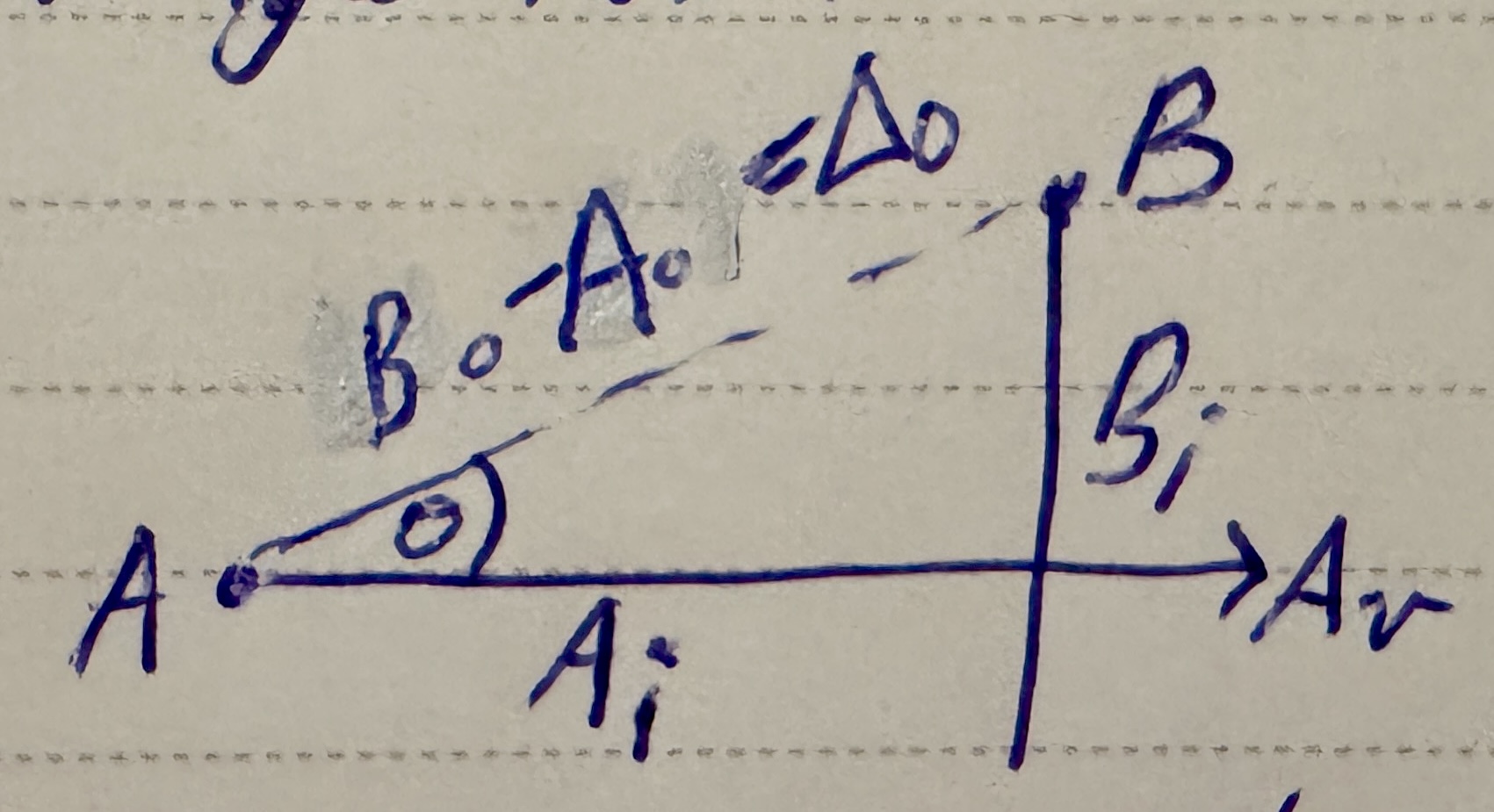
Now we have to work out the time elapsed until A and B hit the intersection point, \(A_t\) and \(B_t\), and then the answer is found by the difference: \(t = |A_t - B_t|\).
Let \(\Delta_0 = B_0 - A_0\).
To find \(A_t\): project \(\Delta_0\) onto \(A_v\) to get the distance between \(A_0\) and the intersection point \(A_i\), and divide that by \(\|A_v\|\) (the speed of A) to get the time elapsed:
$$ A_t = \frac{\Delta_0 . \hat{A_v}}{\|A_v\|} = \frac{\Delta_0 . A_v}{\|A_v\|^2} $$To find \(B_t\): use Pythagoras on the two known sides of the distance triangle and divide that distance by \(V\) (B’s velocity):
$$ B_i = \frac{\sqrt{\Delta_0^2 - A_i^2}}{V} $$Generating test data
How do you make test data for this?
One way is to generate it randomly, through a kind of backwards logic: start at a randomly chosen \(A_0\), travel for randomly chosen \(A_t\) seconds, then travel orthogonally from that for randomly chosen \(B_t\) seconds, then you’re at \(B_0\).
Code shown below (again, in bog-standard python).
# returns (A_0, A_v, B_0, V, t) where t is the time between A and B crossing
# the intersection path. (for checking against output from miss_time_for_intersection_point(...))
def generate_test_data():
space_max = 10
veloc_max = 4
A_0 = (random.uniform(-space_max, space_max), random.uniform(-space_max, space_max))
A_v = (random.uniform(-veloc_max, veloc_max), random.uniform(-veloc_max, veloc_max))
# V is B's speed (> 0)
V = random.uniform(0.01, veloc_max)
# derive B's veloc -- at right angles to A_v.
A_v_orth = (-A_v[1], A_v[0])
A_v_orth_mag = sqrt(A_v_orth[0]**2 + A_v_orth[1]**2)
B_v_unit = (A_v_orth[0] / A_v_orth_mag, A_v_orth[1] / A_v_orth_mag)
B_v = (B_v_unit[0] * V, B_v_unit[1] * V)
# pick how long until A crosses the intersection path
A_t = random.uniform(-50.0, 50.0)
intersection = (A_0[0] + A_t * A_v[0], A_0[1] + A_t * A_v[1])
# pick how long until B crosses intersection path
B_t = random.uniform(0.0, 50.0)
# find B's starting position
B_0 = (intersection[0] - B_t * V * B_v_unit[0],
intersection[1] - B_t * V * B_v_unit[1])
t = abs(A_t - B_t)
return (A_0, A_v, B_0, V, t)
And then you can drive the tests something like:
num_tests = 1000000
epsilon = 1e-5
for i in range(0, num_tests):
(A_0, A_v, B_0, V, t) = generate_test_data()
t_calc = miss_time_for_intersection_point(A_0, A_v, B_0, V)
discrepancy = abs(t_calc - t)
if discrepancy > epsilon:
print(f"Test failed! discrepancy = {discrepancy}")
sys.exit(0)
print(f"All tests passed")
Next time
A future post might go into the higher dimensions problem and the smallest distance between the two particles approach.