Ohmaps: your image montage is a resistor network
Occasionally there’s a lovely moment when I’m working on a problem and I realise I’m also looking at some other thing that seems completely unrelated. It’s like a metaphor made flesh.
These ‘ isomorphism moments’ can be powerful because the two seemingly unrelated things can give you insights into each other. Their commonality encourages you think about the essential thread running through them both.
This post details one of these moments I had recently.
I was playing with ways to make a collection of images into a montage, allowing for scaling of images so they can join together nicely (as long as we preserve aspect ratios — no-one likes squishy images of their cat).
So image size becomes irrelevant and we’re thinking in terms of aspect ratios.
Reminder: aspect ratio is typically defined as \(a = w / h\), the width divided by the height.
One simple scheme is to allow two images1 to be combined horizontally or vertically, resizing the second one to fit the width or height the first (‘edge-fitting’):

If you do some jottings around the aspect ratio equations you’ll find the following equations for joining an arbitrary amount of aspect ratios all together in the same horizontal/vertical way:
$$ \begin{aligned} a_{h} &= a_0 + a_1 + \dots + a_n \\ \\ a_{v} &= \frac{1}{\frac{1}{a_0} + \frac{1}{a_1} + \dots + \frac{1}{a_n}} \end{aligned} $$If you know some simple electronics, you might be seeing something familiar in these equations.
Compare the previous equations to these for simple resistor networks in series and parallel:
$$ \begin{aligned} R_{series} &= R_0 + R_1 + \dots + R_n \\ \\ R_{parallel} &= \frac{1}{\frac{1}{R_0} + \frac{1}{R_1} + \dots + \frac{1}{R_n}} \end{aligned} $$Oho! The same equations. What’s going on here? Is it a ‘coincidence’?
As some great person probably once said, “There are no coincidences in mathematics.”2
I want to speak to the manager
So these two seemingly unrelated worlds have this fundamental connection. That means we might carry information and ideas via this ethereal portal.
We don’t have to look very far to find this other fundamental parallel:
| Aspect ratio | Resistance |
|---|---|
| $$ a = \frac{w}{h} $$ | $$ \quad \text{R} = \frac{\text{V}}{\text{I}} $$ |
So is there some spatial counterpart to voltage and current? No. But there’s something analogous going on when we do edge-fitting of scaled images – it’s that dimension-fitting that is key.
Nature abhors a vacuum
… and electricity doesn’t like gaps in its ledger book.
Consider a connected circuit with flowing current.
At every point, the current going in and out is fully balanced (sums to zero). This is Kirchhoff’s current law (KCL).
For every loop in the circuit, the sum of the voltages is fully balanced (sums to zero). This is Kirchhoff’s voltage law (KVL).
And it all begins to make sense.
Consider some resistor with value \(\text{R}_0\) and draw it on page as a rectangle of aspect \(\text{R}_0\). The width, height of the rectangle are proportional to possible pairs of voltage, current that would be present if connected in a circuit3.
If you scale and horizontally edge-wise join another rectangle for a resistor \(\text{R}_1\) (which has appropriate aspect ratio for its value), you’re effectively joining them in series. The growing or shrinking of the rect for \(\text{R}_1\) in order to join it to \(\text{R}_0\) is preserving the dimension at the vertical edge, which is current in this scheme (and in this way KCL is observed).
Note that the act of growing or shrinking the rectangle for \(\text{R}_1\) also affects the voltage (width), which is correct in the electricity world; the ratio for resistance is maintained this way.
Likewise, if you vertically edge-wise join two rectangles representing resistors, it’s a similar accounting; but the horizontal dimension is preserved this time, which corresponds to voltage (and in this way KVL is observed). This is effectively joining them in parallel.
I heard you like composition
This edge-joining scheme to join resistors in series and parallel composes perfectly to any level. So you can keep on joining rectangles to rectangles (resistors to resistors), edge-wise in either dimension, to build up a picture of resistor networks with series and parallel networks nested.
I’m nicknaming this resistor-network-as-rectangles picture an ohmap, as in ‘ohm-map’4.
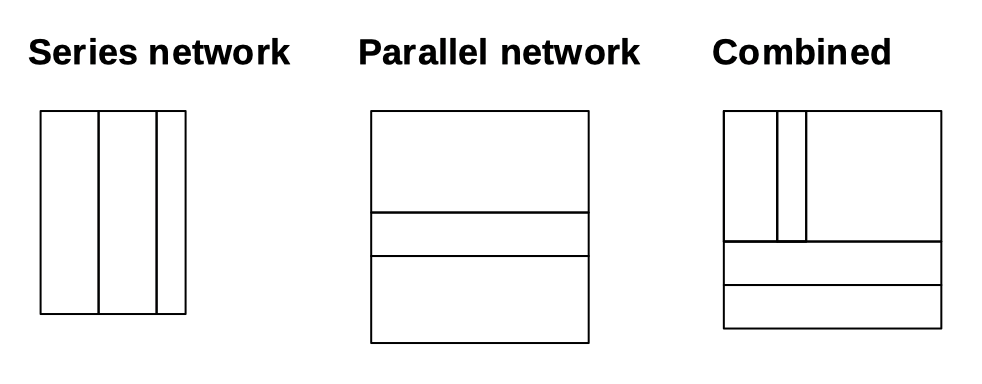
Note that you need to build an ohmap from the bottom-up, since you need to know the aspect ratio (resistance) of sub-networks at the point you join them to other resistors or networks.
The aspect ratio being the resistance applies to rectangles on the page at any level: from the rectangle encompassing the entire network down to single rectangles.
And by extension, you can arbitrarily sub-divide rectangles into more rectangles, or arbitrarily remove sub-rectangles from rectangles, and the overall resistance of the network (the aspect of the bordering rectangle) is the same.
Power move
So if we have voltage and current being the two dimensions of the rectangles there’s another cute correspondence:
| Area | Power |
|---|---|
| $$ \text{A} = wh $$ | $$ \quad \text{P} = \text{V}\text{I} $$ |
An unconnected resistor network doesn’t have any current flowing, hence no power, but we can still consider the relative power dissipation5 in resistor networks. We could make a power dissipation heat map by colouring our rectangles more red according their area percentage of the entire network’s area:
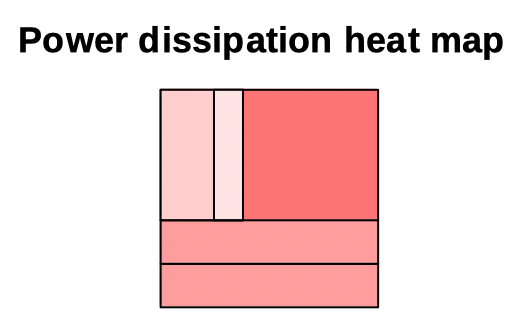
The essential thread
So what is the nucleus here? What mechanism unites image montages and electrical resistance in this way?
I’d say it’s dimension-preserving ratio joining. Any subject matter where you are composing ratios while matching one of the dimensions will be described by those equations.
The exact reason for the ‘dimension preserving’ doesn’t matter. In images, it’s down to aesthetics and practicality; in electrical resistance, it’s about Kirchhoff’s laws, which ultimately is the principle of conservation of energy.
Take it away, Piet
On a final note, let’s just meditate on the fact that Piet Mondrian’s artworks all have an associated resistor network.

Thanks
Thanks go to Ian Stark who I bounced this idea off; he pointed me at the least squares fitting problem, which has some past approaches that are linked to this subject.
More in part 2, part 3, part 4
the two things can be images or already-made montages; only thing that matters is we know the aspect ratio of both ↩︎
but there are mathematical coincidences ( 1 2), which is different ↩︎
of course the average resistor value in a circuit will often be values around the thousands of ohms, so practically speaking you might use kilo-ohms or something higher for the aspect ratios of resistors (to avoid very flat wide rectangles) ↩︎
we’ve reached peakmanteau ↩︎
assuming perfect components, no thermal runaway etc. ↩︎