Ohmaps (part 2)

November 8, 2024

More on Ohmaps: component failure battles, limitations, ambiguity…

Disclaimer: I am not an electrician. Nothing here is electrical advice/expertise. Insure your garments.

Limitations

Not every rectangle picture you can draw represents a circuit. For example, what would this be?¹

And not every resistor network can be shown as an ohmap – things outwith simple series/parallel nestings, like delta or Y networks.

However, there are ways to to convert these to parallel and series representation, then they’re ohmap-able.

Ambiguity

Some ohmaps look ambiguous, like this one:

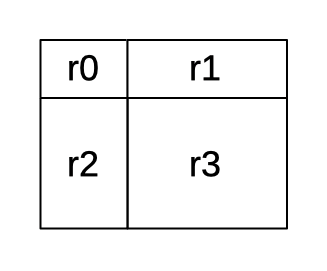
Is this a parallel-inside-series or a series-inside-parallel circuit?

It’s either! It’s both! You can choose, the resulting resistance is the same².

And likewise for any other diagrams that look ambiguous (i.e. with a ‘+’ crossing in them) – all interpretations are valid and end up with the same resistance overall.

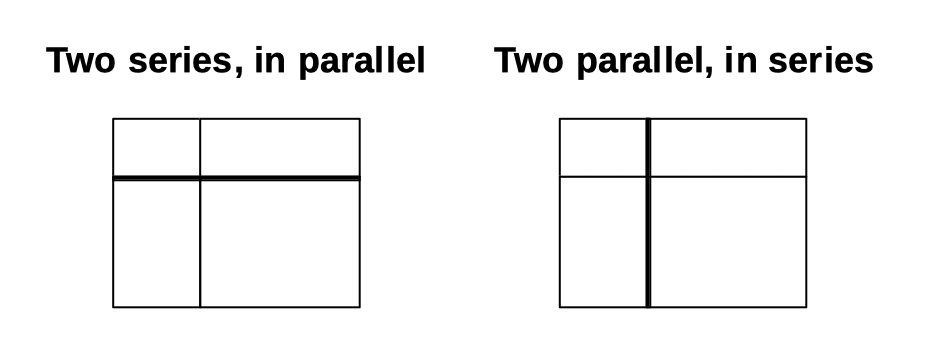
If you ever wanted remove ambiguity for an arrangement, bold lines could be used to show single unbroken edges:

Component failure resolution: let’s do battle!

💡

I think the system below is a cute demonstration of how metaphors can join with e.g. geometry and typography to help make a process or idea memorable.

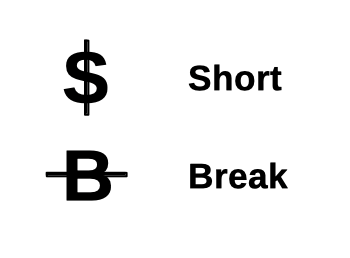
Two basic ways a component can fail in a circuit are:

short: component has zero resistance
break: component has infinite resistance³

The geometric nature of ohmaps offers us an interesting way to see how these kinds of failures resolve using a mnemonic/visual mode of thinking.

The question is: if a component on an Ohmap shorts or breaks, what happens to the circuit?

What would a short look like on an ohmap? A short is zero resistance – think aspect ratio $0/1 = 0 \; \Omega$ – so it would be a vertical line.

What would a break look like on an ohmap? A break is no connection i.e. infinite resistance – akin to aspect ratio $1/0 \Rightarrow \infty \; \Omega$ – so it would be a horizontal line.

Let’s use letters to represent a short and break, but with those lines incorporated in the appropriate directions⁴:

Finally, we need to be aware that any component in an ohmap can be in one of three places:

top level component (the only one) – in which case, if it’s a short or break, game over man, your circuit is dead/battery exploding
part of a horizontal box – i.e. in series with other components
part of a vertical box – i.e. in parallel with other components

If the component is in one of the kinds of box, we must do battle. Here’s how:

The line through the S or B letter is a spear. Think about a real spear: in the direction it points, it’s powerful and defeating (it wins). But side-on, a spear is useless and easily defeated. And that’s how to decide the fate of a box with an S or B inside it:

if the spear points in the direction of the box layout (horizontally or vertically), it defeats the other components in the box – they all disappear, the S or B is the only remaining item
the spear is ‘side on’ to the direction of the box, it’s useless, so the other components ‘defeat’ it – the S or B is removed from the box, leaving everything else in the box

Here’s some sketches of the four possibilities:

And that’s how you do a battle. After a single battle, if the spear ‘won’, do a battle on the new layout. After all battles are resolved, there are two possibilities:

your S or B ends up as the only top-level component: your circuit is bereft of life, it rests in peace, it is an ex-circuit
the S or B was vanquished: you still have some kind of circuit connected⁵

💡

Thinking about how these battles play out: it becomes obvious that a single S or B failure gets its propagation ‘up the box chain’ limited by nesting of series and parallel boxes. If it can defeat its current box, the next box up would be going the other way, and so would defeat the spear.

💡

The vanquishing of components (rectangles) on the ohmap is a qualitative rather than quantitative: which is to say, if you delete any rectangle, the topological view of the circuit is correct, but not necessarily the aspect ratio/resistance. To see the correct resistances after one or more rectangle removals, you need to lay out the ohmap again for the remaining components. But you only need to do it once, after the whole ‘war’ is resolved.

having boldly disparaged this poor picture, I also encourage you sometimes to bloody-mindedly explore the ‘silly things’ and just plow into it and see if you can make it make sense somehow. For a great example of ‘hidden treasure’, see the antimatter prediction of the Dirac Equation, which Dirac didn’t even realise himself until later ↩︎
the two pictures are grouping components by a) same current flow, b) same voltage drop, which obviously might be an interesting detail internally. Moving from (a) to (b) is just the addition of one connection across the middle of the parallel circuit ↩︎
sometimes the word ‘open’ is used on circuit diagrams to show what I call a ‘break’ ↩︎
If there’s any ambiguity in remembering which way the lines go, just think of the S looking like a dollar sign $ – electronics are expensive, right? ↩︎
but what it’s doing is another matter; your 80s memorabilia collection may be at risk of fire ↩︎

Electronics