Xor Xor Gabor
If you’re working with image processing and discrete Fourier transforms (frequency analysis/filtering)1 you need test images, and possibly even videos.
Xor Xor Gabor2 is my name for an easy to make test image (and video) that is a nutritious source of frequencies:
$$ i = x \oplus y \tag{\(0 <= x,y < 2^L\)} $$This is defining the grayscale intensity of a pixel (or square) as the bitwise-XOR of the x and y values.
Here’s how it looks for a couple of different \(L\) (recursion level) values:
Level 3
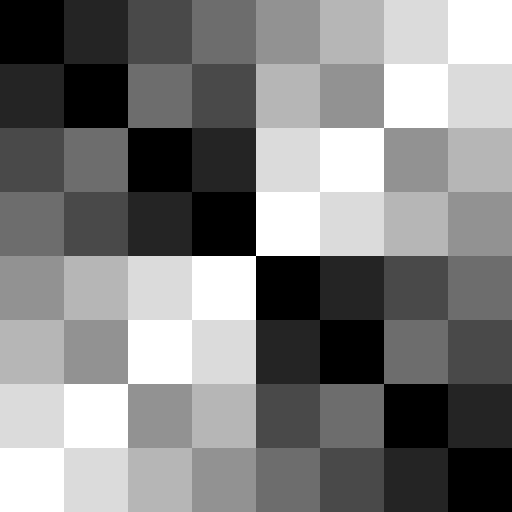
Level 5

Note that we always generate the same image size, e.g. 512 x 512, no matter what the recursion level \(L\), by scaling each square up as necessary.
(Sources available further down)
Xor Xor Gabor as a 3D print
I couldn’t resist making a print of the pattern. Sometimes you just need to see something as a real object!
Grey levels are mapped to height. It’s easier to see various features of Xor Xor Gabor when it’s mapped to height:



With a 3D lit view, you can more easily see that:
- one diagonal of squares are all at the lowest level
- the opposite diagonal of squares are all at the highest level
- there are continuous runs of heights of length \( 2^n \)
Video
If you’re doing time-based analysis/filtering, there’s a video variant that has independent frequencies in the time direction as well as \(x, y\). We just have to xor together all three coordinates3:
where \(t\) represents the 3rd coordinate, time. This maps to the logical frame number for the video frame you’re generating.
I say ‘logical’ frame number because you must take care to not just output each frame once (if each square is larger than 1x1 on your checkerboard) – the amount of times you repeat each frame must match the size of each individual square.
Otherwise, your time frequencies will all be multiplied by \(resolution / 2^L \).
Someone please invent Chessteroids
The gabor image is basically a recursive checkerboard. Checkerboards within checkerboards. This suggests to me a game called chessteroids, the chess and asteroids cross-over that was inevitable:
Imagine variable size chess-ish pieces. You start with the largest. These pieces are homed on the ‘large’ squares (large power of 2 boundaries). When pieces attack each other, they break up into several smaller sized pieces, that are homed on the next level of squares down.
My brain saw it, so you must too.
Source: gabor image generation
import numpy as np
import matplotlib.pyplot as plt
from operator import xor
def generate_checkerboard(size, num_squares):
square_size = size // num_squares
checkerboard = np.zeros((size, size))
for i in range(num_squares):
for j in range(num_squares):
x = xor(i, j)
checkerboard[i * square_size:(i + 1) * square_size, j * square_size:(j + 1) * square_size] = x
return checkerboard
def save_gabor_images(max_level, size=512):
for detail_level in range(1, max_level + 1):
num_squares = pow(2, detail_level)
checkerboard = generate_checkerboard(size, num_squares)
plt.imsave(f'gabor_size{size}_detail{detail_level}.png', checkerboard, cmap='gray', format='png')
def show_gabor_image(level, size=512):
num_squares = pow(2, level)
checkerboard = generate_checkerboard(size, num_squares)
# some fiddling to remove borders and ensure we get 1-1 pixel size on-screen.
# (dpi must be set to something but doesn't change on-screen size)
dpi = 100
fig = plt.figure(figsize=(size / dpi, size / dpi), dpi=dpi)
# Full-figure axes (no padding)
ax = fig.add_axes([0, 0, 1, 1])
ax.imshow(checkerboard, cmap='gray', aspect='auto')
ax.axis('off')
plt.show()
# save all images for detail levels up to 5
save_gabor_images(5)
# show level 3 image in popup
show_gabor_image(5)
Source: gabor video generation
import numpy as np
import matplotlib.pyplot as plt
import cv2
from operator import xor
def generate_checkerboard(size, level, z):
num_squares = pow(2, level)
square_size = size // num_squares
checkerboard = np.zeros((size, size), dtype=np.uint8)
sq_mult = int(256 / (num_squares - 1))
for i in range(num_squares):
for j in range(num_squares):
i_s = min(255, i * sq_mult)
j_s = min(255, j * sq_mult)
zsa_zsa = xor(xor(i_s, j_s), z)
checkerboard[i * square_size:(i + 1) * square_size, j * square_size:(j + 1) * square_size] = zsa_zsa
return checkerboard
def generate_gabor_video(image_size, level, fps):
fps = 30
num_squares = pow(2, level)
num_different_frames = num_squares
square_size = image_size // num_squares
output_filename = 'gabor_video.avi'
fourcc = cv2.VideoWriter_fourcc(*'XVID')
video_writer = cv2.VideoWriter(output_filename, fourcc, fps, (image_size, image_size), isColor=False)
for frame in range(0, num_different_frames):
sq_mult = int(256 / (num_squares - 1))
gabor_image = generate_checkerboard(image_size, level, z=frame*sq_mult)
# We write the same frame the same amount of times as a square's size,
# to maintain the same frequencies across space and time (equal pixel-to-frame ratio)
for i in range(0, square_size):
video_writer.write(gabor_image)
generate_gabor_video(image_size=512, level=5, fps=30)
Document history
- 2024-11-15
- published
- 2026-02-18
- added photos of 3D print